Тема 2.
Бинарное счисление.
Перевод чисел в двоичную, десятичную
и шестнадцатеричную систему счисления.

Предмет Булевой Алгебры - действия с числами в бинарном счислении.
Чтобы отобразить десятичное число в бинарном виде, следует записать
его как позиционно-отображаемое число с базой 2.
Для этого следует помнить, что любая позиционная система счисления
основана на записи цифр числа в ряд, когда каждая последующая цифра
умножается на базовое число (в двоичном (бинарном) счислении это 2)
в степени позиции (разряда) по возрастанию справа налево, начиная с 0.

В двоичной системе базой является число 2. Так же как в 10-ном
счислении привычной нам - является число 10.
Единственными цифрами в двоичной системе счисления являются "0" и "1"
В цифровой технике "0" или "1" носит называние бит. Число из 8 цифровых
разрядов носит название байт.
1024 байт = 1 килобайт, 1024 килобайт = 1 мегабайт.
Двоичная (бинарная) система счисления необходима в вычислительной технике
потому, что цифровая техника представляет «ноль» как уровень напряжения
0 вольт и «единицу» как уровень напряжения 5 вольт ( в более новой
технике «единица» может быть представлена и более низкими уровнями 3.3В ,
1.8В , 1.2В и так далее для экономии энергопотребления).
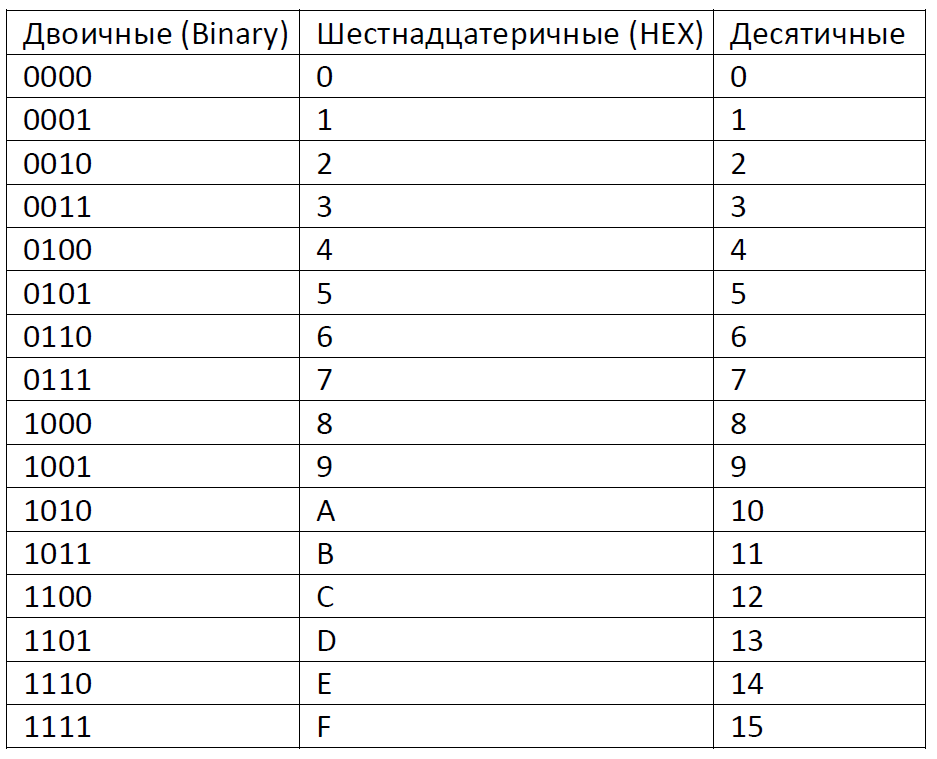
Двоичным числом из 8 разрядов (бит) можно представить числа от 0 до 255.
Двоичным числом из 4 разрядов (бит) можно представить числа от 0 до 15
Поэтому в в вычислительной технике помимо двоичной системы счисления
используется ещё гексадецимальная (шестнадцатиничная) система счисления,
позволяющая наиболее удобно представлять двоичные 4-х и 8-и битовые
двоичные числа.
11000110 (BIN)= C6 (HEX)
С бинарными числами можно проводить математические и логические действия.

bermanalexandr@gmail.com
Телефон администратора этой странички: +7 9827458948.